`$\newcommand{\N}{\mathbb{N}} \newcommand{\Z}{\mathbb{Z}} \newcommand{\Q}{\mathbb{Q}} \newcommand{\R}{\mathbb{R}} \newcommand{\LP}{\left(} \newcommand{\RP}{\right)} \newcommand{\LS}{\left\lbrace} \newcommand{\RS}{\right\rbrace} \newcommand{\LA}{\left\langle} \newcommand{\RA}{\right\rangle} \newcommand{\LB}{\left[} \newcommand{\RB}{\right]} \newcommand{\MM}{\ \middle|\ } \newcommand{\exp}{\text{exp}} \newcommand{\abs}[1]{\left\vert#1\right\vert} \newcommand{\msr}[1]{m\left(#1\right)} \newcommand{\inv}[1]{#1^{-1}} \newcommand{\bkt}[1]{\LA \img{#1}\RA} \require{color}$`s

The Tanglenomicon

A table of two string tangles

The algebraic tangles

Zachary Bryhtan, Nicholas Connolly, Isabel Darcy, Paria Karimi, Ethan Rooke, Joseph Starr*

Mathematics Department at The University of Iowa

Joint Math Meetings 2025 (1/10/25)

Tangles

“We define a tangle as a portion of a knot diagram from which there emerge just 4 arcs pointing in the compass directions NW, NE, SW, SE.” - Conway, J.H.

Basic Operations

Operation $+$

Operation $\vee$

Algebraic Tangles

All possible tangles made from $+$ and $\vee$ on basic tangles

But actually arborescent

Arborescent knots (and tangles) are constructed by taking a collection of twisted bands described by a weighted tree and connecting them with successive plumbing.

It’s straight forward to see (you should see in the example) that algebraic and arborescent constructions describe the same class of object.

Anatomy of a tree

Rings

Linearization of Arborescent tangles

$\pm$ Abbreviated Canonical Tangle Trees

• Weight Condition At each vertex of $\Gamma$, at most one weight is non-zero.
• Stick Condition On any stick the weights are non-zero except for end vertices that have a bond free in $\Gamma_0$ and for the case $\Gamma_0=\alpha(0[0])$, $\Gamma_0=\alpha[0]$. The non-zero weights along any stick are of alternating sign. No end vertex of a stick has weight $\pm 1$ unless it has a bond free in $\Gamma_0$, or $\Gamma_0=[\pm 1]$.
• One of:
  • Positivity Condition There are no sticks in $\Gamma_0$ of the form $[-1],\ [ -2],\ \alpha[-2],\ \alpha[2]\alpha$.
  • Negative Condition There are no sticks in $\Gamma_0$ of the form $[1],\ [ 2],\ \alpha[2],\ \alpha[2]\alpha$
• Abbreviation Condition A vertex of $\Gamma_0$ of ring number $1$ has valence $\geq 2$, and $\Gamma_0$ is not $\alpha\langle 2\ 0\rangle$. Every ring subtree of $\Gamma$ is adjacent to a non-essential vertex.

Rational Tangle Trees

Montesinos Tangle Trees

Constructing an arborescent tangle

Game plan

1. Find a way to generate abstract rooted trees
2. Modify that method to get tangle trees

Building a tangle tree

1. List the integral tangles
2. Find the trees
3. Find the ornaments
4. Hang the ornaments on the trees

The integral 4 tangle

Call the CACN of a tree $T$ and the CACN of an ornament $O$. For the tangle generated by hanging an ornament to have $\text{CACN}=4$ we need $T+O=4$.

Additionally, hanging an ornament must satisfy the stick condition. Meaning:

• $1<O\leq 4=\text{CACN}$ and $0\leq T<4$
• Signs of weights on an ornament may need to be adjusted.$\text{Example: }[1\ -2\ 3]\to [-1\ 2\ -3]$
• Tangles with root which is weight $0$ and non-essential are excluded, except $\iota[0]$.

This gives the following for $T$ and $O$:

Tangles of canonical arborescent

crossing number up to 4

Using The Tanglenomicon

Alpha

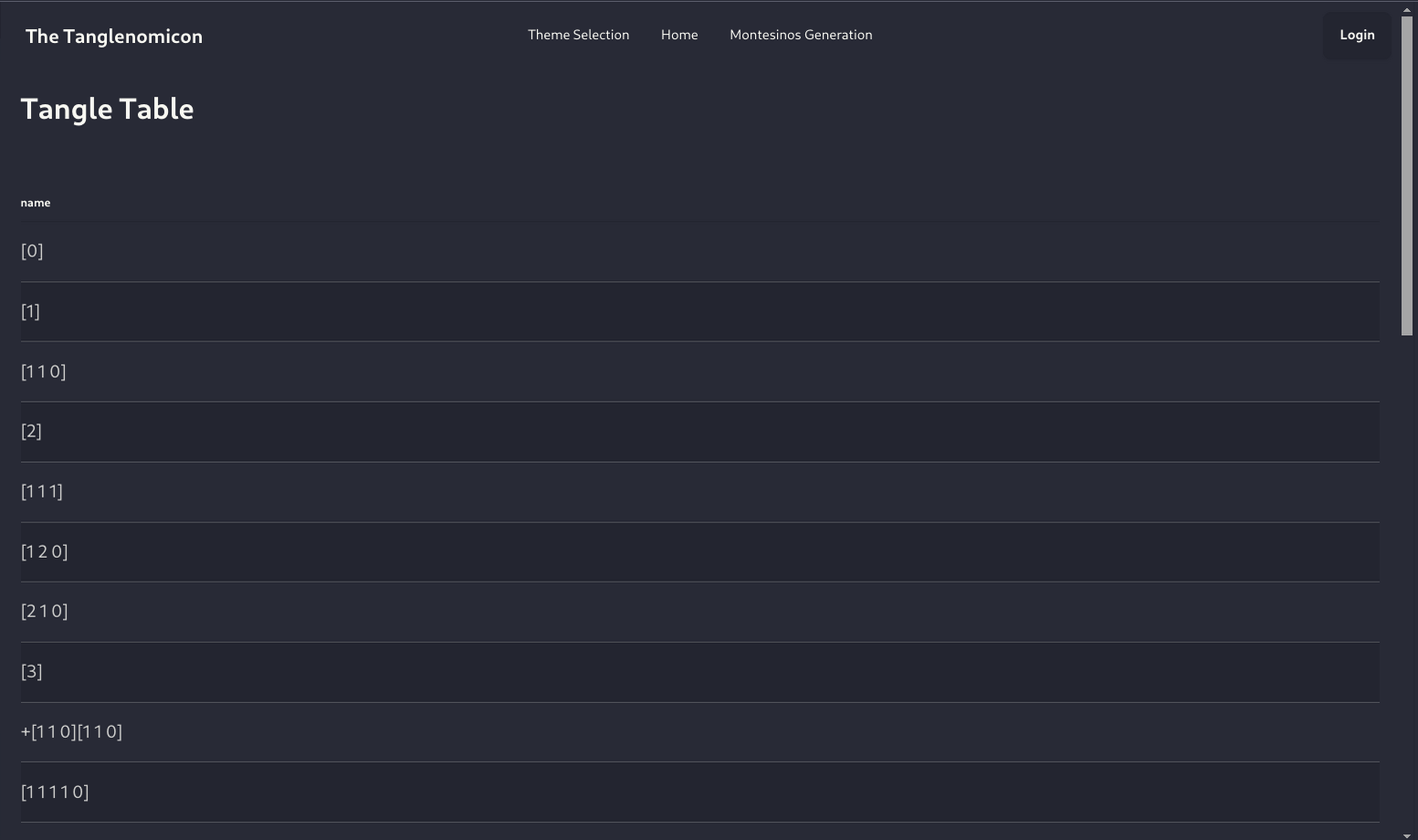
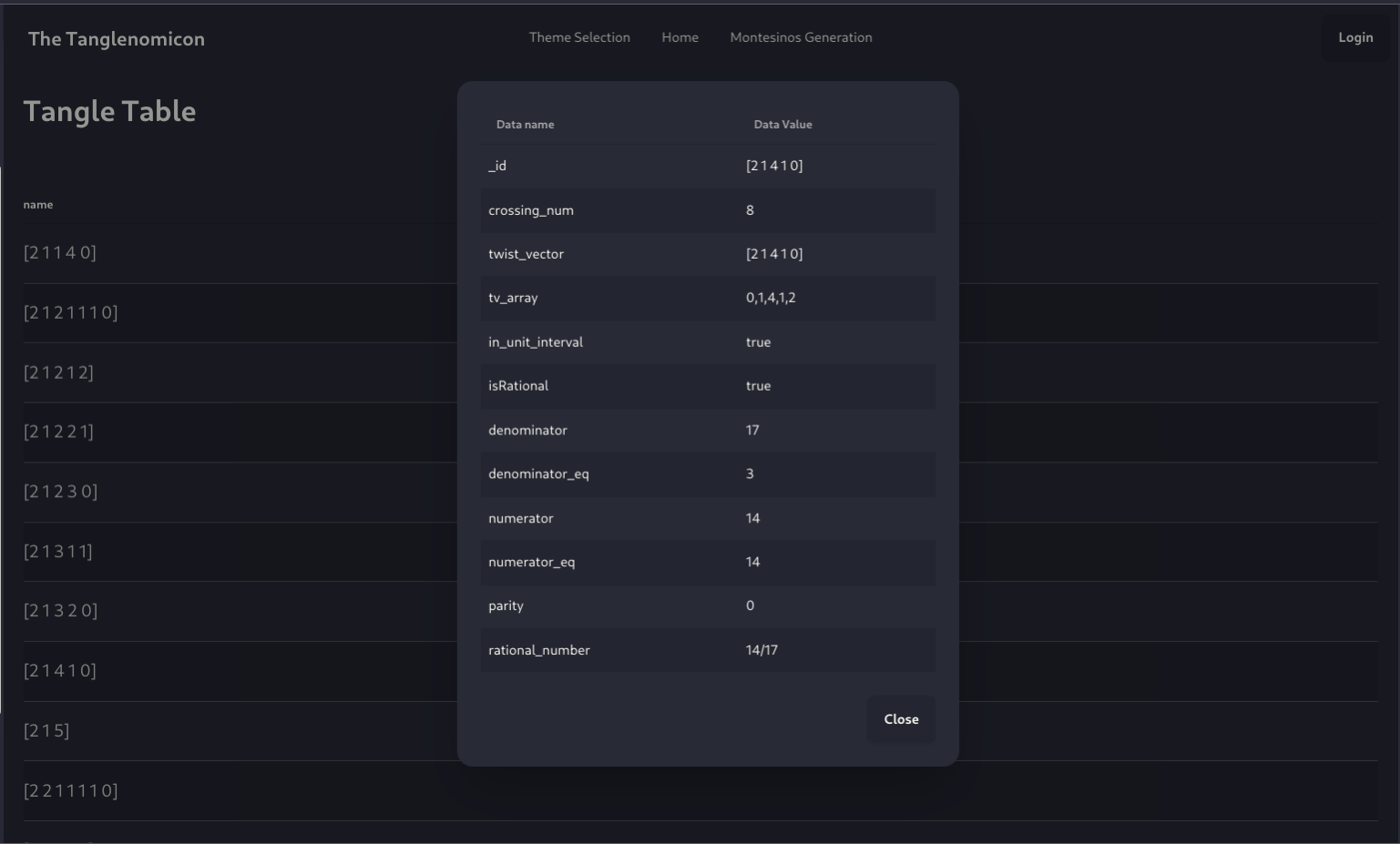
To play with a live version, visit: