`$\newcommand{\N}{\mathbb{N}} \newcommand{\Z}{\mathbb{Z}} \newcommand{\Q}{\mathbb{Q}} \newcommand{\R}{\mathbb{R}} \newcommand{\LP}{\left(} \newcommand{\RP}{\right)} \newcommand{\LS}{\left\lbrace} \newcommand{\RS}{\right\rbrace} \newcommand{\LA}{\left\langle} \newcommand{\RA}{\right\rangle} \newcommand{\LB}{\left[} \newcommand{\RB}{\right]} \newcommand{\MM}{\ \middle|\ } \newcommand{\exp}{\text{exp}} \newcommand{\abs}[1]{\left\vert#1\right\vert} \newcommand{\msr}[1]{m\left(#1\right)} \newcommand{\inv}[1]{#1^{-1}} \newcommand{\bkt}[1]{\LA \img{#1}\RA} \require{color}$`s

U of M - Dearborn Colloquium (11/15/23)

The Tanglenomicon

Zachary Bryhtan, Nicholas Connolly, Isabel Darcy, Ethan Rooke, Joseph Starr*

Mathematics Department at The University of Iowa

Knots

“A knot is a smooth embedding of a circle $S^1$ into Euclidean 3-dimensional space $\R^3$ (or the 3-dimensional sphere $S^3$ ).”

Knot Equivalence

reidemeister moves

Type I

Type II

Type III

The natural question

Knot Tables

• 1860’s Tait computes knots up to 7 crossing
  • 15 knots
• 1870’s Tait, Kirkman, and Little compute knots up to 10 crossing
  • Takes about 25 years
  • 250 knots
• 1960’s Conway computes knots up to 11 crossings
  • “A few hours”
  • 802 knots

• 1980’s Dowker and Thistlethwaite compute up to 13 crossings
  • First using a computer
  • 12,966
• 1990’s Hoste, Thistlethwaite, and Weeks compute up to 16 crossings
  • Computer runtime on the order of weeks
  • 1,701,936
• 2020’s Burton computes up to 19 crossings
  • 350 Million

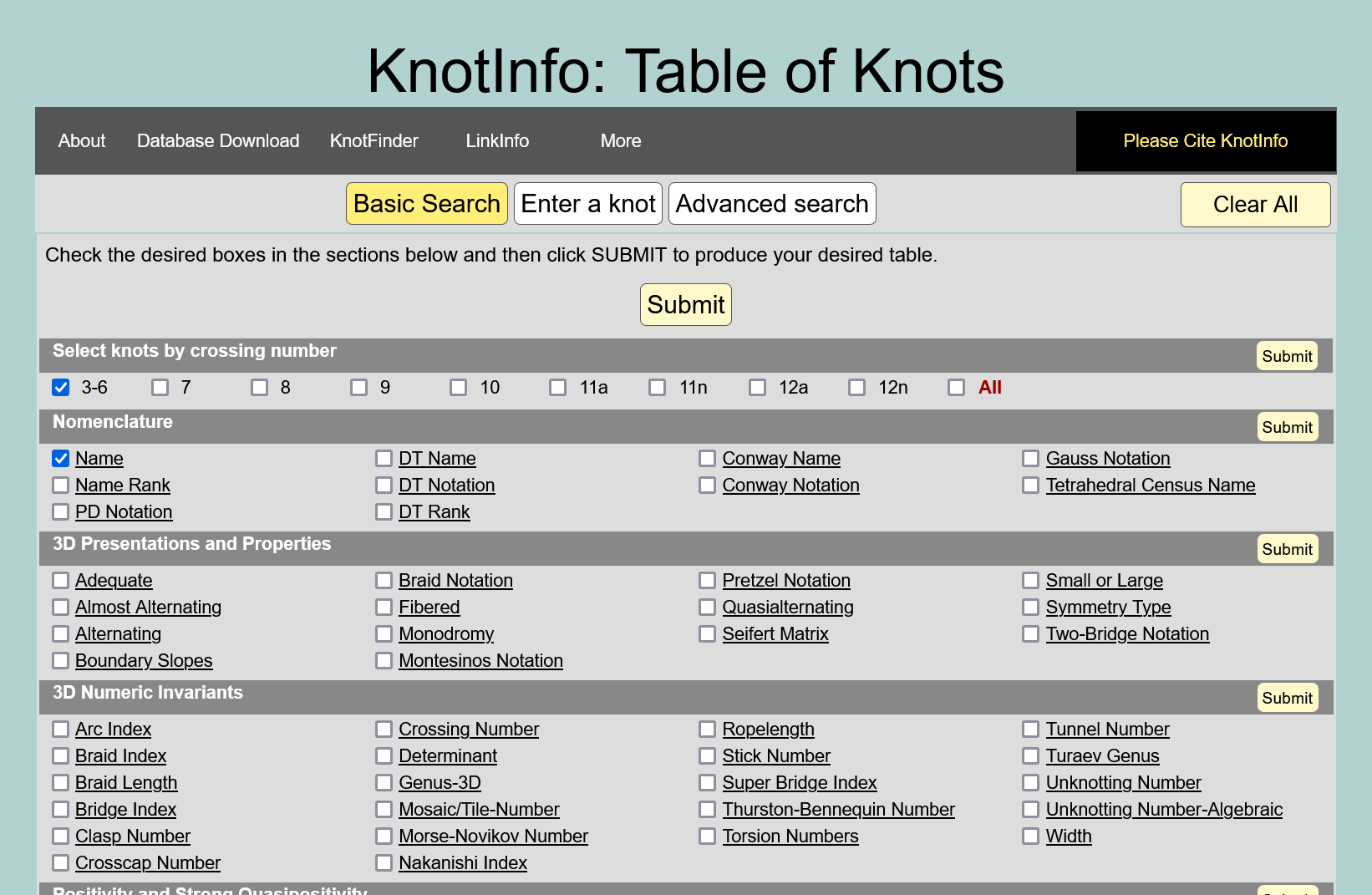
KnotInfo

Conway

Tangles

“We define a tangle as a portion of a knot diagram from which there emerge just 4 arcs pointing in the compass directions NW, NE, SW, SE.”

Basic Operations

Operation $+$

Operation $\vee$

The Tanglenomicon

Building up

Where we are

Rational Tangles

Generation

For any $N$ an obvious twist vector is the twist vector of all $1$s $$[1\ 1\ 1\ \cdots\ 1]$$ Noting that when we write this sequence we have $N-1$ spaces.

If we choose to place a $+$ instead of the left most space we get $$[1+1\ 1\ \cdots\ 1]=[2\ 1\ \cdots\ 1]$$ we’re free to make this choice for each space

this gives $N-1$ choices between ‘$+$’ and space $$[1\square 1\square 1\square\cdots\square1]$$ letting us generate twist vectors by simply counting from $0\to 2^{N-1}$.

Canonical Twist Vectors

We can write a canonical twist vector by taking the odd length vectors (appending $0$ where needed).

Programmatic Description

Computations

Rational Number (continued fraction)

The rational number for a twist vector is computed by taking the twist vector as a finite continued fraction that is: $$\LB a\ b\ c\RB=c+\frac{1}{b+\frac{1}{a}}$$

To play with twist vectors and continued fractions visit